Durbin-Watson Test

Basic Concepts

The Durbin-Watson Test is used to determine whether there is first-order autocorrelation, which occurs when there is a (linear) correlation between the error term for one observation and the error term for the next observation. This is especially relevant with time series data where the data are sequenced by time.

The Durbin-Watson test uses the following statistic:

where the e_i = y_i – ŷ_i are the residuals, n = the number of elements in the sample, and k = the number of independent variables. Hypothesis testing using the Durbin Watson statistics assumes that the residuals are normally distributed.

d takes on values between 0 and 4. A value of d = 2 means there is no autocorrelation. A value substantially below 2 (and especially a value less than 1) means that the data is positively autocorrelated, i.e. on average, a data element is close to the subsequent data element. Finally, a value of d substantially above 2 means that the data is negatively autocorrelated, i.e. on average a data element is far from the subsequent data element.

Example

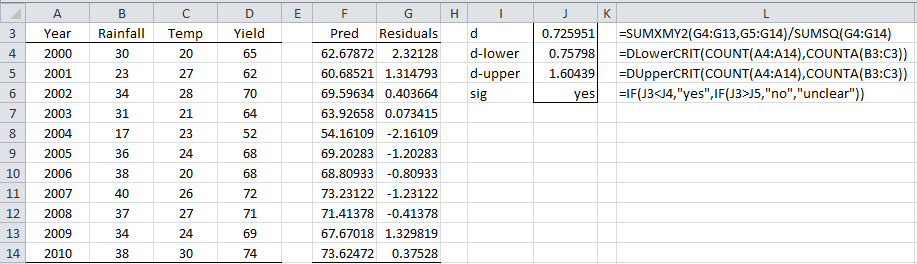
Example 1: Find the Durbin-Watson statistic for the data in Figure 1.

Figure 1 – Durbin-Watson Test

The d statistic (cell J3) is 0.725951, but what does this tell us about the autocorrelation?

Property

Property 1: For large n, the following is true

d ∼ N(2, 2/√n)

In this case, the normal approximation of the critical value d_crit is

NORM.INV(α,2,2/SQRT(n))

Values of d < d_crit indicate a significant autocorrelation.

Hypothesis Testing

We can use the Durbin-Watson statistic for significance testing based on the Durbin-Watson Table. For each value of alpha (.01 or .05) and each value of the sample size n (from 6 to 2000) and each value of the number of independent variables k (from 1 to 20), the table contains a lower and upper critical value (d_L and d_U).

Since most regression problems involving time-series data show a positive autocorrelation, we usually test the null hypothesis H₀: the autocorrelation ρ ≤ 0 (which we believe is ρ = 0) versus the alternative hypothesis H₁: ρ >  0, using the following criteria:

If d < d_L reject H₀ : ρ ≤ 0 (and so accept H₁ : ρ > 0)

If d > d_U do not reject H₀ : ρ ≤ 0 (presumably ρ = 0)

If d_L < d < d_U test is inconclusive

Note that if d > 2 then we should test for negative autocorrelation instead of positive autocorrelation. To do this, simply test 4–d for positive autocorrelation as described above.

For Example 1, with α = .05, we know that n = 11 and k = 2. From the Durbin-Watson Table, we see that d_L = .75798 and d_U = 1.60439. Since d = 0.72595 < .75798 = d_L, we reject the null hypothesis, and conclude that there is a significant positive autocorrelation.

More Examples

Suppose that n = 100, k = 5 and d = 1.8. From Durbin-Watson Table for α = .05, we see that d_L = 1.623 and d_U = 1.725. Since d = 1.8 > 1.725 = d_U, we cannot reject the null hypothesis that there is no autocorrelation.

For large values of n, we can also use Property 1. This time we see that d_crit = NORM.INV(.05,2,2/SQRT(100)) = NORM.INV(.05,2,.2) = 1.67 < 1.8 = d, and so once again we see that we cannot reject the null hypothesis. Of course, for values of d between dL and dU the normal approximation would give a definitive result, while the analysis using the table would give an inconclusive result. As we can see from the table in Durbin-Watson Table, the smaller the value for k then less of a problem this is.

Now suppose that n = 2200, k = 5 and d = 1.97. Since n > 2000, we can’t use the table of critical values, and so we must use the normal approximation. We see that d_crit = NORM.INV(.05,2,2/SQRT(2200)) = 1.93 < 1.97 = d, and so once again we see that we cannot reject the null hypothesis.

Worksheet Functions

Real Statistics Function: The following two versions of the DURBIN function are available in the Real Statistics Resource Pack.

DURBIN(R1) = the Durbin-Watson statistic d where R1 is a column vector containing residuals

DURBIN(R1, R2) = the Durbin-Watson statistic d where R1 is a m × n range containing X data and R2 is an m × 1 column vector containing Y data.

DLowerCRIT(n, k, α, h) = lower critical value of the Durbin-Watson statistic  for samples of size n (6 to 2,000) based on k independent variables (1 to 20) for α = .01, .025 or .05 (default). If h = TRUE (default) harmonic interpolation is used; otherwise linear interpolation is used.

DUpperCRIT(n, k, α, h) = upper critical value of the Durbin-Watson statistic  for samples of size n (6 to 2,000) based on k independent variables (1 to 20) for α = .01, .025 or .05 (default). If h = TRUE (default) harmonic interpolation is used; otherwise linear interpolation is used.

Actually, the DURBIN function is an array function, described as follows:

DURBIN(R1, R2, lab, α): returns a column range with the values d, d_L, d_U and sig where R1 is a m × n range containing X data and R2 is an m × 1 column vector containing Y data,

DURBIN (R1, k, lab, α): returns a column range with the values d, d_L, d_U and sig where R1 is a column vector containing residuals and k = the # of independent variables (default = 2)

Details

Here α = .01, .025 or .05 (default). If lab = TRUE (default = FALSE) then an extra column of labels is added to the output.

Note that the functions DLowerCRIT and DUpperCRIT support a much larger range of values of n than the Durbin-Watson Table. Also these functions support α = .01, .025 and .05 (actually any value between .01 and .05 by using interpolation), while the table only provides values for α = .01 and .05.

Examples

Referring to Figure 1, we can calculate the statistic d = 0.72595 using either one of the formulas: = DURBIN(G4:G14) or =DURBIN(B4:C14,D4:D14). In fact, if we highlight the range I3:J6 and enter either of these formulas and then press Ctrl-Shft-Enter the result will be the same as shown in range I3:J6 of Figure 1.

Data Analysis Tool

Real Statistics Data Analysis Tool: The Linear Regression data analysis tool provided by the Real Statistics Resource Pack also supports the Durbin-Watson Test as described next.

To conduct the test in Example 1, press Ctrl-m and double click on the Linear Regression data analysis tool. Now fill in the dialog box that appears as shown in Figure 2.

Figure 2 – Durbin-Watson data analysis

The output is similar to that generated by the formula

=DURBIN(B4:C14,D4:D14,TRUE,O24)

Test for Large Samples

For n > 200, you can test the null hypothesis that there is no autocorrelation by noting that based on this null hypothesis the following test statistic has a standard normal distribution

where df = n – k – 1 (n = sample size and k = # of independent variables). Thus, if ABS(z) > NORM.S.INV(α/2), then you reject the null hypothesis and conclude that there is autocorrelation.

For sample sizes 200 ≥ n ≥ 50, you can use the following test statistic instead

where c = 0.0026991244575048159 + 3.11878179323157 / df

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2018) Durbin-Watson statistic
https://en.wikipedia.org/wiki/Durbin%E2%80%93Watson_statistic

Lee, M-Y. (2016) On the Durbin Watson statistic based on a Z-test in large samples, Int. J. Computational Economics and Econometrics, Vol. 6, No. 1, pp.114-121.
https://ideas.repec.org/a/ids/ijcome/v6y2016i1p114-121.html