Binomial Distribution

Characteristics of a binomial distribution

Definition 1: Suppose an experiment has the following characteristics:

  • the experiment consists of n independent trials, each with two mutually exclusive possible outcomes (which we will call success and failure)
  • for each trial, the probability of success is p (and so the probability of failure is 1 – p)

Each such trial is called a Bernoulli trial. Let x be the discrete random variable whose value is the number of successes in n trials. Then the probability distribution function for x is called the binomial distribution, B(n, p), whose frequency function (aka probability density function) is

f(x) = C(n, x)px(1–p)n–x

where C(n, x) = \frac{n!}{x!(n-x)!} and n! = n(n–1)(n–2)⋯3∙2∙1 as described in Combinatorial Functions.

C(n, x) can be calculated by using the Excel function COMBIN(n,x). See Figure 2 of Built-in Excel Functions for more details about this function.

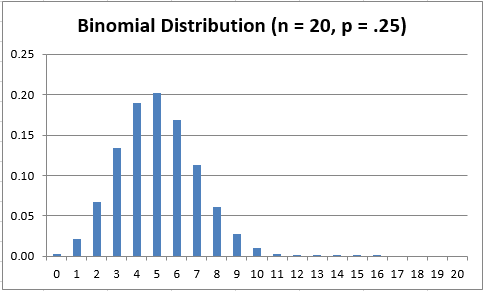
Figure 1 shows a graph of the probability density function for B(20, .25).

Figure 1 Binomial distribution

That the graph looks a lot like the normal distribution is not a coincidence (see Relationship between Binomial and Normal Distributions)

Mean and Variance

Property 1:

Mean = np

Var = np(1–p)

Click here for a proof of Property 1.

Excel Worksheet Functions

Excel provides the following functions regarding the binomial distribution:

BINOM.DIST(x, n, p, cum) = the probability density function value f(x) for the binomial distribution  (i.e. the probability that there are x successes in n trials where the probability of success on any trial is B(n, p) when cum = FALSE and the corresponding cumulative probability distribution value F(x) (i.e. the probability that there are at most x successes in n trials where the probability of success on any trial is p) when cum = TRUE.

BINOM.INV(n, p, 1 – α) = critical value; i.e. the smallest value of x such that F(x) ≥ 1 – α, where F is the cumulative binomial distribution function for B(n, p)

These functions are not supported for versions of Excel prior to Excel 2010; the following functions are used instead: BINOMDIST, which is equivalent to BINOM.DIST, and CRITBINOM, which is equivalent to BINOM.INV.

Excel 2013 introduces the following new function (where x ≤ y ≤ n):

BINOM.DIST.RANGE(n, p, x, y) = the probability there are between x and y successes (inclusive) in n trials where the probability of success on any single trial is p

Thus, BINOM.DIST.RANGE(n, p, x, y) = BINOM.DIST(y, n, p, TRUE) – BINOM.DIST(x–1, n, p, TRUE) if x > 0 and BINOM.DIST.RANGE(n, p, 0, y) = BINOM.DIST(y, n, p, TRUE). The y parameter may be omitted, in which case BINOM.DIST.RANGE(n, p, x) = BINOM.DIST(x, n, p, FALSE).

Examples

Example 1: What is the probability that when you throw a die 10 times it will come up six 4 times?

We can model this problem using the binomial distribution B(10, 1/6) as follows

image515

Alternatively, the problem can be solved using the Excel formula:

BINOM.DIST(4, 10, 1/6, FALSE) = 0.054266

Example 2: What is the probability that heads come up more than tails in 20 tosses of a fair coin?

Let E1 = the event that heads come up more than tails, E2 = the event that tails come up more than heads, and E3 = the event that heads comes up just as many times as tails. First note that P(E1) = P(E2) and P(E1) + P(E2) + P(E3) = 1, and so P(E1) = (1–P(E3))/2. Now

P(E_3)

P(E_1)

Critical values of a discrete distribution

Because the binomial distribution is discrete, the values calculated by BINOM.INV (or CRITBINOM) may not always represent the critical values.  E.g. suppose you are conducting a two-tailed test with n = 100, p = .4 and α = .05, then BINOM.INV(100, .4, .025) = 31. But note that

         BINOM.DIST(31,100,0.4,TRUE) = .03985

         BINOM.DIST(30,100,0.4,TRUE) = .02478

Since .02478 ≤ .025 = α/2, the lower critical value is 30 and not 31. In fact, the lower critical value is always 1 less than the value calculated by BINOM.INV, except in the case where the value is calculated by =BINOM.DIST(x, n, p, TRUE) is exactly α/2, in which case, x = BINOM.INV(n, p, α/2); and so, in this case, you shouldn’t subtract 1.

It turns out that the upper critical value is indeed the one calculated by BINOM.INV. In the example given above, BINOM.INV(100, .4, .975) = 50 and

         BINOM.DIST(50,100,0.4,TRUE) = .9832

         BINOM.DIST(49,100,0.4,TRUE) = .9729

Since .9832 ≥ .975 = 1 – α/2, but .9729 < .975, the critical value is in fact 50.

Real Statistics Function

The Real Statistics Resource Pack provides the following function that implements the above process to identify the appropriate critical value.

BINOM_CRIT(n, p, α): if α < .5 then the left critical value is returned, while if α ≥ .5, then the right critical value is returned.

If you are employing a two-tailed test, then you must substitute α/2 for α to get the left critical value and substitute 1–α/2 for α to get the right critical value.

For the previous example given above, we get BINOM_CRIT(100,.4,.025) = 30 and BINOM_CRIT(100,.4,.975) = 50.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Forbes, C. Evans, M, Hastings, N., Peacock, B. (2011) Statistical distributions. 4th Ed, Wiley
https://www.wiley.com/en-us/Statistical+Distributions%2C+4th+Edition-p-9780470390634

Wikipedia (2012) Binomial distribution
https://en.wikipedia.org/wiki/Binomial_distribution

155 thoughts on “Binomial Distribution”

  1. 1.You make widgets. You want to sell your widgets at the nearby widget store, since this would potentially increase your sales. However, you would have to pay a transportation cost every day to send you widgets over to the store. You decide to run some calculations to see if you would be at risk of losing money due to the transportation costs.
    You know that 5 other widget companies sell widgets at that store, so you would be the 6th. Assuming a customer is equally likely to select any of the widgets, what is the probability they will select and purchase your widget? Write your answer as a probability (not a percent) rounded to 4 decimals.
    2.The widget store owner tells you that 200 customers arrive and purchase a widget from the store each day. Assuming you must sell 30 of your widgets to cover the transportation costs, and given the probability you calculated in question 1, use a binomial distribution to estimate the probability of at least covering the transportation costs (that is, the probability of selling at least 30 widgets). Write your answer as a probability (not a percent) rounded to 4 decimals.

    3.How many minimum number of people would have to visit the store to give you at least a 0.95 probability of covering the transportation costs? HINT: Use the BINOM.DIST function trying out various values for “n”, the number of trials.

    4.The widget store manager points out that not all widget brands get equal purchase rates. A brand on premium shelf space has a 0.28 probability of being selected by each customer. He is willing to give you premium shelf space at the front of the store for a small fee. The additional fee, plus the original transportation costs, would raise the minimum number of widgets you would have to sell to 40 (to cover transportation costs and additional fee).
    Assuming 200 customers come into the store, use a binomial distribution to estimate the probability of at least covering the transportation costs and additional fee. Write your answer as a probability (not a percent) rounded to 4 decimals.

    5.The widget store manager reminds you that while the average number of people that show up each day is 200, the actual number varies. He tells you that the customers that show up each day can be modelled with a Poisson distribution where lambda = 200. What is the probability that at least 200 customers arrive (that is, either 200 or more than 200 customers arrive)? Write your answer as a probability (not a percent) rounded to 4 decimals.

    6.How many minimum number of people would have to visit the store to give you at least a 0.95 probability of covering the transportation costs and the additional fee? Use as 0.28 the probability of a widget being selected by a person. HINT: You need to sell at least 40 widgets to cover transportation cost and the additional fee. So, the number of “successes” need to be greater than equal to 40. The probability of “success” in each trial is 0.28. Now use the BINOM.DIST function trying out various values for “n”, the number of trials.

    7.You are curious about the accuracy of the estimates that the widget store owner gave you. If you wanted to take a random sample of daily customer arrivals, from which of the following is the population you should sample?
    The number of arrivals each day for this widget store and the competing widget store down the street.
    The number of arrivals each day for all days this specific widget store has been open.
    The number of arrivals each day for this specific widget over the past month.
    A random, representative sample of the number of arrivals each day to this specific widget store.
    8.The store owner gives you data on customer arrivals over the last 3 years. You randomly select a sample of daily customer arrivals, and then take the mean of that sample. If you were to repeat this process multiple times, you would expect the distribution of the sample means to be:
    A Normal Distribution
    A Binomial Distribution
    A Poisson Distribution
    The same distribution as the population of interest
    9.
    Question 9
    Assuming the widget store owner’s original estimates (given in Question 5) are accurate, what would you expect the mean of the distribution above to be?

    Reply

  2. You make widgets. You want to sell your widgets at the nearby widget store, since this would potentially increase your sales. However, you would have to pay a transportation cost every day to send you widgets over to the store. You decide to run some calculations to see if you would be at risk of losing money due to the transportation costs.
    You know that 5 other widget companies sell widgets at that store, so you would be the 6th. Assuming a customer is equally likely to select any of the widgets, what is the probability they will select and purchase your widget? Write your answer as a probability (not a percent) rounded to 4 decimals.

    Reply

Leave a Reply to Charles Cancel reply