One-Sample Anderson-Darling Test

Objective

The Anderson-Darling test has a similar objective to that of the Kolmogorov-Smirnov test, but it is more powerful. This is so since all the data values are considered, not just the one that produces the maximum difference. Also, more weight is given to the tails of the distribution being fitted. Generally, this test should be used instead of the Kolmogorov-Smirnov test. Unlike the version of the one-sample Kolmogorov test described on this website, the approach used varies based on the theoretical distribution being fitted.

How to Perform the Test

Suppose you want to see how well sample X fits a continuous distribution with cumulative distribution function (cdf) F(x). To perform the one-sample Anderson-Darling test, first sort the sample X in increasing order: x₁ ≤ x₂ ≤ … ≤ x_n and then calculate the following statistic

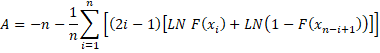
Specified Parameters

We start with a distribution function F(x) that is fully determined (i.e. none of the parameters need to be estimated from the sample). Figure 1 displays the critical values in this case, at least for large samples, although usually, samples of size n > 7 will suffice. We will refer to such a distribution as generic or specified.

Figure 1 – Anderson-Darling critical values

As for the KS test, there is a significant difference between the sample data and the theoretical distribution provided A ≥ c.

Actually, we can use the AD_DIST(x) and AD_INV(p) functions to obtain more accurate estimates of the critical values and p-values. Click here for details.

The critical values and p-values are also valid when the data is fitted to a uniform distribution between 0 and 1 (e.g. when determining whether the data is random).

Estimated Parameters

When the parameters of the distribution are not known but need to be estimated from the sample, we need to perform a few additional steps. First, we calculate the test statistic AD based on A, but which may be modified depending on the specific distribution, as described in Figure 2.

Figure 2 – Anderson-Darling test statistic

For the gamma distribution, k is the shape parameter, referred to as α in Gamma Distribution.

We determine that there is a significant difference between the sample data and the theoretical distribution provided AD ≥ crit, where crit is the critical value (for a given value of α) defined based on the table of critical values shown in Anderson-Darling Statistical Table.

Normal Distribution

Note that for the normal distribution, the critical value is given by

where a, b, and d are shown in the table of critical values shown in Anderson-Darling Statistical Table.

For the normal distribution, p-values can be obtained from Figure 3.

AD	p-value
AD ≤ .2	1 – exp(-13.436 + 101.14 AD – 223.73 AD2)
.2 < AD ≤ .34	1 – exp(-8.318 + 42.796 AD – 59.938 AD2)
.34 < AD < .6	exp(0.9177 – 4.279 AD – 1.38 AD2)
AD ≥ .6	exp(1.2937 – 5.709 AD + 0.0186 AD2)

Figure 3 – p-values for normal distribution

Example

Example 1: Repeat Example 2 of Kolmogorov-Smirnov Test for Normality using the Anderson-Darling test for normality (the data is repeated in range A4:A18 of Figure 4).

Figure 4 – Anderson-Darling test for normality

We insert formula =NORM.DIST(A4,$G$3,$G$4,TRUE) in cell C4 and the formula =LARGE($C$4:$C$18,B4) in cell D4. Then we highlight range C4:D18 and press Ctrl-D. The Anderson-Darling A statistic is shown in cell G12 and the modified version AD is shown in cell G13. The p-value (cell G14) is calculated as described in Figure 3 (using range G7:G10). Finally, the critical value (cell G20) is calculated using the a, b, and d critical values from the table of critical values in Anderson-Darling Statistical Table.

Note that p-value = .040459, and so we conclude that the data is significantly different from normality. This result is similar to the p-value = .043227 that we obtained from the Shapiro-Wilk test in Example 2 of Shapiro-Wilk Test.

Note too that the same test can be used for the lognormal distribution. For data {x₁, …, x_n} you simply test {ln x₁, …, ln x_n} for a fit with the normal distribution.

Worksheet Functions

Real Statistics Functions: The following functions are provided in the Real Statistics Pack:

ANDERSON(R1, dist, k) = the Anderson-Darling D statistic for the theoretical cdf values in range R1 (assumed to be sorted in ascending order) based on the distribution defined by dist.

ADCRIT(n, alpha, dist, k, interp) = the critical value for the Anderson-Darling test for the distribution specified by dist.

ADPROB(x, dist, k, iter, interp, txt) = an approximate p-value for the Anderson-Darling test at x (which is set to the AD statistic)  for the specified distribution, based on an interpolation of the critical values in the table in Anderson-Darling Statistical Table, using iter number of iterations (default = 40) to calculate the approximation.

ADTEST(R1, dist, lab, iter, alpha): returns an array with the Anderson-Darling D statistic, the critical value, and the estimated p-value for the Anderson-Darling test on the data in range R1 (not necessarily in sorted order) based on the stated distribution dist.

Function arguments

The dist parameter takes the values shown in Figure 5.

Figure 5 – dist values

n is the sample size. This value must be supplied for the normal, lognormal, Laplace, Cauchy, and Generalized Pareto distributions. It is ignored and can be omitted for the other distributions. For the Laplace or Generalized Pareto distributions, n must take a value ≥ 10 (and ≤ 100 for the GPD). For the Cauchy distribution, n must take a value ≥ 5.

k = the shape parameter (alpha) of the gamma distribution (default 1) and is ignored for the other distributions with the following exception. k is also used in the ADPROB function for the Laplace, Cauchy, and Generalized Pareto distributions where k = the sample size, which must take a value in the ranges described for n above,

alpha is the significance level (default .05). If interp = TRUE then harmonic interpolation is used in calculating the critical value; otherwise, linear interpolation is used. If lab = TRUE (default FALSE), then an extra column of labels is appended to the output from ADTEST to yield a 3 × 2 range.

As described earlier on this webpage, the Anderson-Darling test statistic requires the calculation of the natural log. If the log of zero or a negative number is required, then the ANDERSON and ATEST functions will return an error value.

Alpha ranges

Note that the values for α in the table of critical values in Anderson-Darling Statistical Table range from .01 to .15 for the generic distribution, from .0025 to .25 for the exponential distribution, from .005 to .25 for the gamma distribution, from .005 to .20 for the normal distribution, and from .01 to .25 for the other distributions.

When txt = FALSE (default) for values of x smaller than the lower limit, the value of  =ADPROB(x, n, dist, k, iter, interp) is artificially set to 0, and for values of x bigger than the upper limit, the value of this formula is set to 1. When txt = TRUE, then the output takes a  form such as “< .01” or “> .25”.

Arguments for the ADTEST function

For ADTEST, dist and alpha are as described above. ADTEST returns a column array with the values AD statistic, p-value, and critical value. If lab = TRUE (default FALSE), then a column of labels is appended to the output.

R1 is a column array or range that contains the sample data. The exception is the generic case, where R1 contains the theoretical cdf values. Note that for the uniform distribution, which is assumed to be on the interval (0,1), the sample and theoretical cdf values are the same.

For the ADTEST function for the Generalized Pareto distribution, the location parameter μ for the data in R1 must be zero (otherwise, you must subtract μ from all the sample data values).

iter argument for the ADTEST function

iter is used to determine the distribution parameters for the specified distribution (defined by dist). If iter > 0 then these parameters are estimated using the maximum likelihood estimate (MLE) based on the GAMMA_FIT, WEIBULL_FIT, etc. functions using the default argument values except that the number of iterations is set to the iter value (see Distribution Fitting via the MLE).

If iter = 0 or -1 then the distribution parameters are estimated using the method of moments based on the GAMMA_FITM, WEIBULL_FITM, etc. functions using the default argument values except that if iter = -1 then the pure argument is set to TRUE (see Distribution Fitting via the Method of Moments).

For the Cauchy distribution (dist = 12 or “cauchy”), then if iter = 0, then the trim mean estimate is used, while if iter = -1 then the median estimate is used; in either case, the exclusive version of the IQR is used.

If iter = -2 then the distribution parameters are estimated by the WEIBULL_FITR and CAUCHY_FITX functions using the default arguments. In fact, iter = -2 is only used for the Weibull or Cauchy distributions.

Alternative form of the ADTEST function

Note that if the default WEIBULL_FIT, GAMMA_FITM, etc. argument values, as described above, don’t yield the desired result, you can separately estimate the distribution parameters and then use the following alternative version of the ADTEST function.

ADTEST(R1, dist, lab, , alpha, param1, param2)

If param1 is specified then the value of iter is ignored and the distribution parameter values are those specified by param1 and, if necessary, by param2. Note that this form can’t be used for dist = 0 or “specified”, or for dist = 6 or “uniform”. For the uniform distribution, the parameters are automatically set to 0 and 1. For the specified case, no parameters are used since R1 contains the theoretical cdf values and so these don’t need to be estimated from the distribution parameters.  

Alternative Analysis

For Example 1, the value in cell G13 can be computed by =ANDERSON(C4:C18,1). Note that the cell range corresponds to the F(x) values in column C, not the data values in column A.

Here, the F(x) values are based on the sample mean and standard deviation. If instead, we wanted to test whether the data in range A4:A18 of Figure 4 was a good fit for a normal distribution with mean 4 and standard deviation 2, we would use the analysis shown in Figure 6.

Figure 6 – Anderson-Darling test for a generic distribution

Example using worksheet functions

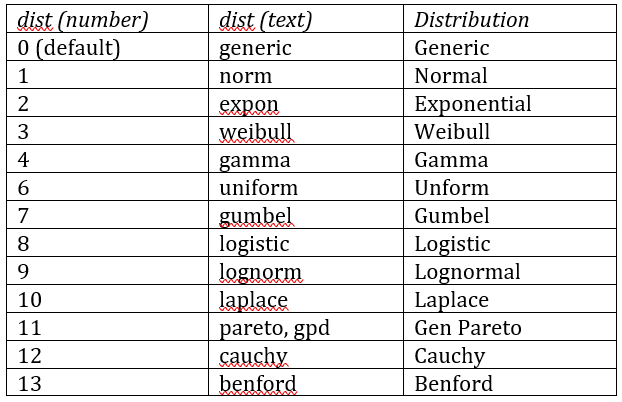
Example 2: Test whether the data in range A4:A18 of Figure 7 is a good fit for the gamma distribution.

Figure 7 – Anderson-Darling test for gamma distribution

This time, we use the ADTEST array function to compute the p-value for the test. Since p-value = “>.25”, we conclude that the gamma value is a good fit for the data. Note that p-value = “>.25” simply means that the calculated Anderson-Darling statistic (.3901) is less than the smallest value on the table of critical values, which in this case is .475 (when α = .25 for k = 3, the value in cell F4). Thus, we really know that p-value >> .25.

We would have gotten the same result for the p-value by using the formula =ADPROB(F9,4,F4). Note that this time, we need to explicitly refer to the k value in cell F4. We could have calculated the Anderson-Darling statistic by using the formula =ANDERSON(C4:C18,4,F4).

Note that while the ANDERSON function uses the theoretical F(x) values (column C), ADTEST uses the data values (column A). The only exception to this is for a test of a generic distribution (i.e. one where there are no unknown parameters). In this case, ADTEST must reference the theoretical F(x) values. E.g. to calculate the results shown in range F9:F11 of Figure 6, we could use the array formula =ADTEST(C4:C18,,TRUE).

Data Analysis Tool

You can also perform the One-sample Anderson-Darling Test via the Goodness of Fit data analysis tool. Click here for more information about this data analysis tool.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Ang, A. H. and Tang, W. H. (2006) Probability Concepts in Engineering: Emphasis on Applications in Civil & Environmental Engineering

Pettitt, A.N. (1976) A two-sample Anderson-Darling rank statistic. Biometrika (1976) 63 (1): 161-168
https://academic.oup.com/biomet/article/63/1/161/236401/A-two-sample-Anderson-Darling-rank-statistic

Stephens, M.A. (1979) The Anderson-Darling statistic. Technical Report No. 39. Stamford University.
https://archive.org/details/DTIC_ADA079807/page/n19/mode/2up

Puig, P. and Stephens, M. A. (2000) Tests of fit for the Laplace distribution, with applications
Available from Researchgate